方差分析(Analysis of Variance，简称ANOVA)，又称“F检验”，是R.A.Fisher发明的，用于两个及两个以上样本均数差别的显著性检验。它是以F值为统计量的计量资料的假设检验方法。检验方法是将总方差分解成两个或多个部分方差和，推断两组或多组的总体无数是否相等。

完全随机设计方差分析的应用条件:n各样本是相互独立的随机样本；n各组样本均来自正态总体；n各组的总体方差相等。另外各单元格样本含量比较大(>30)且各单元格样本含量相同的情况下，方差是否相等对结果影响几乎没有。

例题：研究某机关工作人员血脂水平，随机抽取不同年龄组男性各10名，检测他们的总胆固醇（TC）的含量(mmol/L)，其结果如下：

A组 5.01 4.85 4.93 5.18 4.95 4.78 5.18 4.89 5.07 5.21

B组 5.12 5.13 4.89 5.20 4.99 5.14 5.16 4.98 5.16 5.25

C组 5.24 5.26 5.23 5.11 5.31 5.23 5.21 4.98 5.15 5.19

问题：三个年龄组的总胆固醇平均含量之间的差别是否有统计学意义？进一步两两比较结果如何？

1 录入数据，建立变量分组以及指标，见图1。

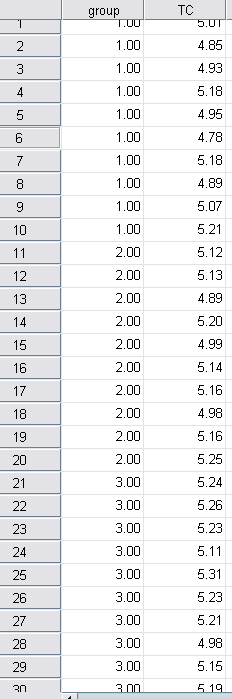
图1

2 在SPSS软件工具栏中按图示依次点击Analyze »Compare Means »One-Way ANOVA开始检验，见图2。

图2

3 Dependent List选TC,Factor选group,点击Post Hoc勾选LSD，S-N-K，Dunnett，然后continue，见图3。

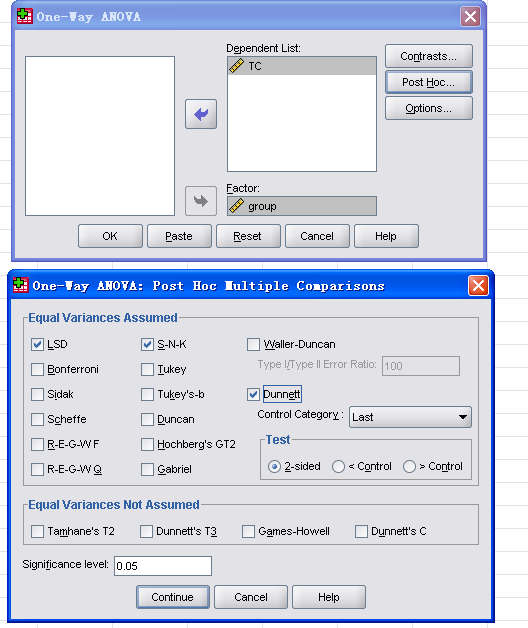
图3

4 点击Options，勾选Descriptive和Homogeneity，然后continue，见图4。

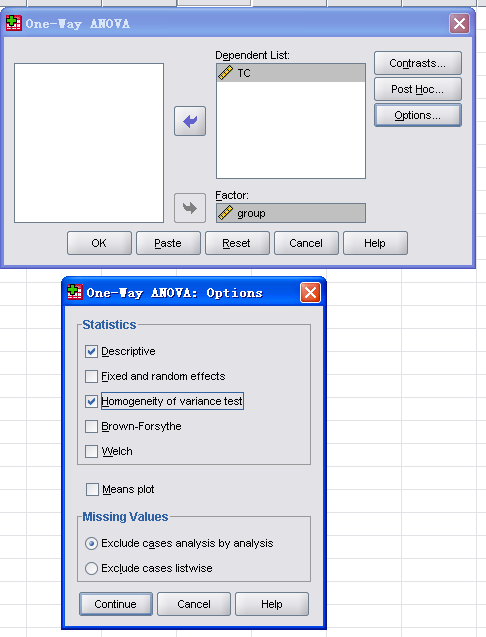
图4

5 选完上面这些，就可以点击“OK”了，这时结果就出来了（图5和6），可以看到到每组的均数和标准差，得出F=5.920，P=0.007，在检验水准为0.05的水平下，差异有统计学意义，可以认为三组的TC水平不全相等。进一步两两比较显示，1（A组）和3（C组）之间TC水平差异有统计学意义，其余组间比较均无差异，见图6。

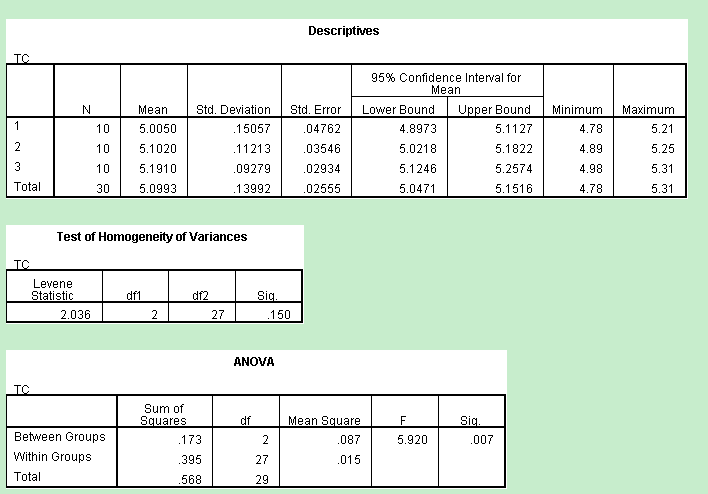
图5

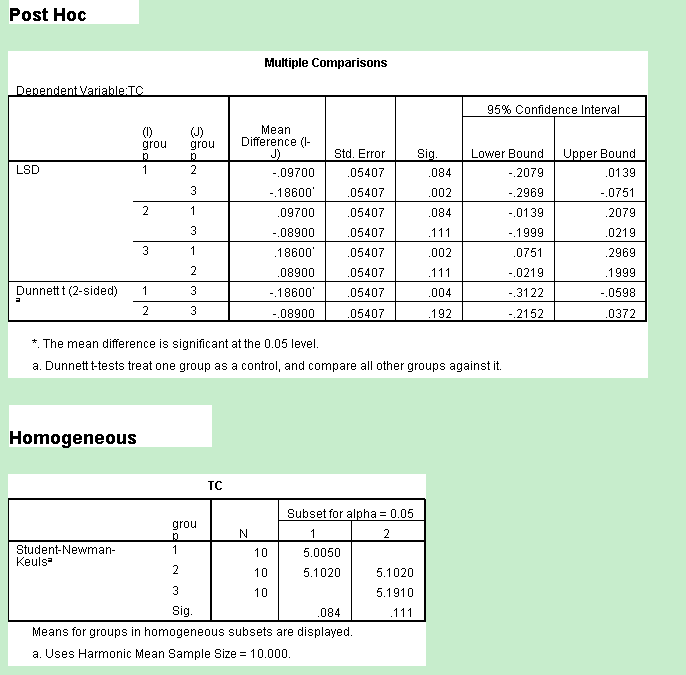
图6